How to Read a Closed End Manometer

Gases

Gas Force per unit area

OpenStaxCollege

[latexpage]

Learning Objectives

By the end of this section, you volition be able to:

• Define the property of pressure
• Define and convert amid the units of pressure level measurements
• Describe the operation of mutual tools for measuring gas force per unit area
• Calculate pressure from manometer data

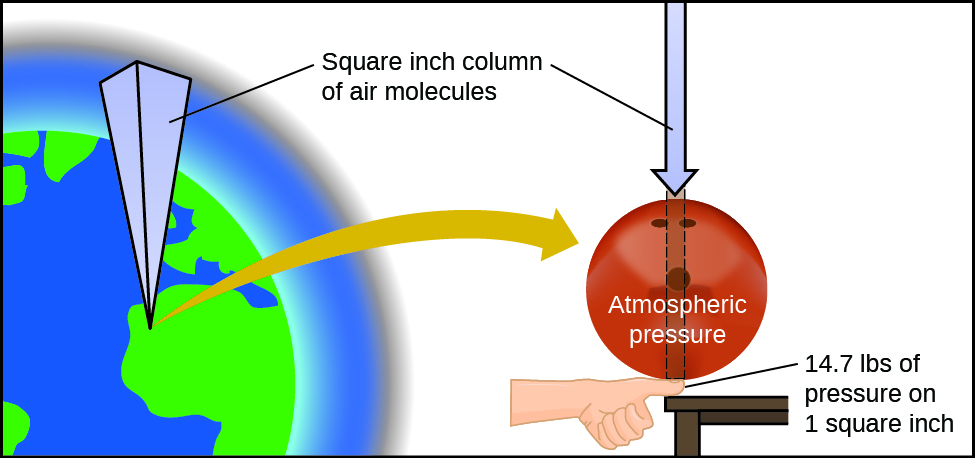
The earth's atmosphere exerts a pressure, as does any other gas. Although we exercise not usually notice atmospheric pressure level, we are sensitive to pressure changes—for instance, when your ears "popular" during accept-off and landing while flying, or when you swoop underwater. Gas force per unit area is caused past the force exerted by gas molecules colliding with the surfaces of objects ([link]). Although the force of each collision is very small, any surface of appreciable surface area experiences a big number of collisions in a short fourth dimension, which tin can result in a high force per unit area. In fact, normal air pressure level is potent plenty to crush a metal container when non balanced by equal pressure from within the container.

The atmosphere to a higher place us exerts a big force per unit area on objects at the surface of the earth, roughly equal to the weight of a bowling ball pressing on an expanse the size of a human thumbnail.

A dramatic illustration of atmospheric pressure is provided in this brief video, which shows a railway tanker car imploding when its internal force per unit area is decreased.

A smaller scale demonstration of this phenomenon is briefly explained.

Atmospheric pressure is caused by the weight of the cavalcade of air molecules in the atmosphere to a higher place an object, such as the tanker machine. At body of water level, this pressure is roughly the same equally that exerted by a full-grown African elephant continuing on a doormat, or a typical bowling ball resting on your thumbnail. These may seem like huge amounts, and they are, simply life on earth has evolved under such atmospheric force per unit area. If you actually perch a bowling ball on your thumbnail, the pressure level experienced is twice the usual pressure, and the sensation is unpleasant.

In full general, pressure is defined equally the force exerted on a given area: \(P=\phantom{\dominion{0.2em}{0ex}}\frac{F}{A}.\) Annotation that pressure is straight proportional to force and inversely proportional to area. Thus, pressure can exist increased either by increasing the corporeality of strength or past decreasing the expanse over which it is applied; pressure tin can be decreased past decreasing the force or increasing the surface area.

Allow's apply this concept to decide which would be more likely to fall through thin ice in [link]—the elephant or the figure skater? A large African elephant can weigh 7 tons, supported on 4 anxiety, each with a bore of well-nigh one.5 ft (footprint area of 250 in²), so the pressure level exerted past each foot is about 14 lb/in²:

\(\text{pressure per elephant human foot}=\text{xiv,000}\phantom{\rule{0.2em}{0ex}}\frac{\text{lb}}{\text{elephant}}\phantom{\dominion{0.4em}{0ex}}×\phantom{\rule{0.4em}{0ex}}\frac{\text{1 elephant}}{\text{4 feet}}\phantom{\rule{0.4em}{0ex}}×\phantom{\rule{0.4em}{0ex}}\frac{\text{1 foot}}{250\phantom{\rule{0.2em}{0ex}}{\text{in}}^{2}}\phantom{\dominion{0.2em}{0ex}}=xiv\phantom{\dominion{0.2em}{0ex}}{\text{lb/in}}^{2}\)

The figure skater weighs about 120 lbs, supported on two skate blades, each with an expanse of about 2 in^two, so the pressure exerted past each bract is well-nigh thirty lb/inⁱⁱ:

\(\text{pressure per skate blade}=120\phantom{\dominion{0.2em}{0ex}}\frac{\text{lb}}{\text{skater}}\phantom{\dominion{0.4em}{0ex}}×\phantom{\rule{0.4em}{0ex}}\frac{\text{i skater}}{\text{2 blades}}\phantom{\rule{0.4em}{0ex}}×\phantom{\dominion{0.4em}{0ex}}\frac{\text{1 blade}}{2\phantom{\rule{0.2em}{0ex}}{\text{in}}^{2}}\phantom{\rule{0.2em}{0ex}}=30\phantom{\rule{0.2em}{0ex}}{\text{lb/in}}^{2}\)

Even though the elephant is more than than i hundred-times heavier than the skater, information technology exerts less than half of the pressure and would therefore be less likely to fall though thin ice. On the other hand, if the skater removes her skates and stands with bare feet (or regular footwear) on the ice, the larger area over which her weight is applied greatly reduces the pressure exerted:

\(\text{pressure per homo human foot}=120\phantom{\dominion{0.2em}{0ex}}\frac{\text{lb}}{\text{skater}}\phantom{\rule{0.4em}{0ex}}×\phantom{\rule{0.4em}{0ex}}\frac{\text{1 skater}}{\text{ii feet}}\phantom{\dominion{0.4em}{0ex}}×\phantom{\rule{0.4em}{0ex}}\frac{\text{ane human foot}}{30\phantom{\rule{0.2em}{0ex}}{\text{in}}^{2}}\phantom{\rule{0.2em}{0ex}}=2\phantom{\rule{0.2em}{0ex}}{\text{lb/in}}^{2}\)

Although (a) an elephant's weight is large, creating a very large force on the footing, (b) the effigy skater exerts a much higher pressure level on the ice due to the pocket-sized surface area of her skates. (credit a: modification of piece of work by Guido da Rozze; credit b: modification of work by Ryosuke Yagi)

The SI unit of pressure is the pascal (Pa), with 1 Pa = 1 N/m², where N is the newton, a unit of force divers as 1 kg m/s². One pascal is a minor force per unit area; in many cases, it is more user-friendly to use units of kilopascal (i kPa = yard Pa) or bar (i bar = 100,000 Pa). In the Us, force per unit area is often measured in pounds of forcefulness on an surface area of one foursquare inch—pounds per square inch (psi)—for example, in car tires. Pressure tin also be measured using the unit atmosphere (atm), which originally represented the average sea level air pressure level at the approximate latitude of Paris (45°). [link] provides some data on these and a few other common units for pressure measurements

Pressure Units
Unit of measurement Name and Abbreviation	Definition or Relation to Other Unit of measurement
pascal (Pa)	one Pa = 1 N/chiliadtwo recommended IUPAC unit
kilopascal (kPa)	1 kPa = m Pa
pounds per foursquare inch (psi)	air pressure at ocean level is ~14.seven psi
temper (atm)	i atm = 101,325 Pa air pressure at sea level is ~1 atm
bar (bar, or b)	1 bar = 100,000 Pa (exactly) commonly used in meteorology
millibar (mbar, or mb)	1000 mbar = 1 bar
inches of mercury (in. Hg)	one in. Hg = 3386 Pa used past aviation industry, also some weather reports
torr	\(\text{i torr}=\phantom{\rule{0.2em}{0ex}}\frac{\text{1}}{\text{760}}\phantom{\rule{0.2em}{0ex}}\text{atm}\) named after Evangelista Torricelli, inventor of the barometer
millimeters of mercury (mm Hg)	1 mm Hg ~one torr

Conversion of Force per unit area Units
The United States National Weather Service reports force per unit area in both inches of Hg and millibars. Convert a pressure of 29.two in. Hg into:

(a) torr

(b) atm

(c) kPa

(d) mbar

Solution
This is a unit of measurement conversion problem. The relationships between the various pressure units are given in [link].

(a) \(29.two\phantom{\dominion{0.2em}{0ex}}\overline{)\text{in Hg}}\phantom{\dominion{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\frac{\text{25.iv}\overline{)\text{mm}}}{ane\phantom{\dominion{0.2em}{0ex}}\overline{)\text{in}}}\phantom{\rule{0.2em}{0ex}}\phantom{\rule{0.2em}{0ex}}×\phantom{\dominion{0.2em}{0ex}}\frac{\text{ane torr}}{1\phantom{\rule{0.2em}{0ex}}\overline{)\text{mm Hg}}}\phantom{\rule{0.2em}{0ex}}=\text{742 torr}\)

(b) \(742\phantom{\dominion{0.2em}{0ex}}\overline{)\text{torr}}\phantom{\rule{0.2em}{0ex}}×\phantom{\dominion{0.2em}{0ex}}\frac{\text{1 atm}}{760\phantom{\rule{0.2em}{0ex}}\overline{)\text{torr}}}\phantom{\dominion{0.2em}{0ex}}=\text{0.976 atm}\)

(c) \(742\phantom{\rule{0.2em}{0ex}}\overline{)\text{torr}}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\frac{\text{101.325 kPa}}{760\phantom{\rule{0.2em}{0ex}}\overline{)\text{torr}}}\phantom{\rule{0.2em}{0ex}}=\text{98.9 kPa}\)

(d) \(98.9\phantom{\rule{0.2em}{0ex}}\overline{)\text{kPa}}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\frac{1000\phantom{\rule{0.2em}{0ex}}\overline{)\text{Pa}}}{1\phantom{\rule{0.2em}{0ex}}\overline{)\text{kPa}}}\phantom{\rule{0.4em}{0ex}}×\phantom{\rule{0.4em}{0ex}}\frac{1\phantom{\dominion{0.2em}{0ex}}\overline{)\text{bar}}}{100,000\phantom{\rule{0.2em}{0ex}}\overline{)\text{Pa}}}\phantom{\dominion{0.4em}{0ex}}×\phantom{\rule{0.4em}{0ex}}\frac{\text{g mbar}}{one\phantom{\dominion{0.2em}{0ex}}\overline{)\text{bar}}}\phantom{\rule{0.2em}{0ex}}=\text{989 mbar}\)

Check Your Learning
A typical barometric pressure in Kansas Metropolis is 740 torr. What is this pressure in atmospheres, in millimeters of mercury, in kilopascals, and in bar?

Answer:

0.974 atm; 740 mm Hg; 98.7 kPa; 0.987 bar

We tin measure atmospheric pressure, the strength exerted past the temper on the earth's surface, with a barometer ([link]). A barometer is a glass tube that is airtight at one stop, filled with a nonvolatile liquid such equally mercury, and so inverted and immersed in a container of that liquid. The atmosphere exerts force per unit area on the liquid outside the tube, the column of liquid exerts pressure level inside the tube, and the pressure at the liquid surface is the same within and outside the tube. The acme of the liquid in the tube is therefore proportional to the pressure exerted by the atmosphere.

In a barometer, the height, h, of the column of liquid is used as a measurement of the air force per unit area. Using very dense liquid mercury (left) permits the construction of reasonably sized barometers, whereas using water (right) would require a barometer more 30 feet tall.

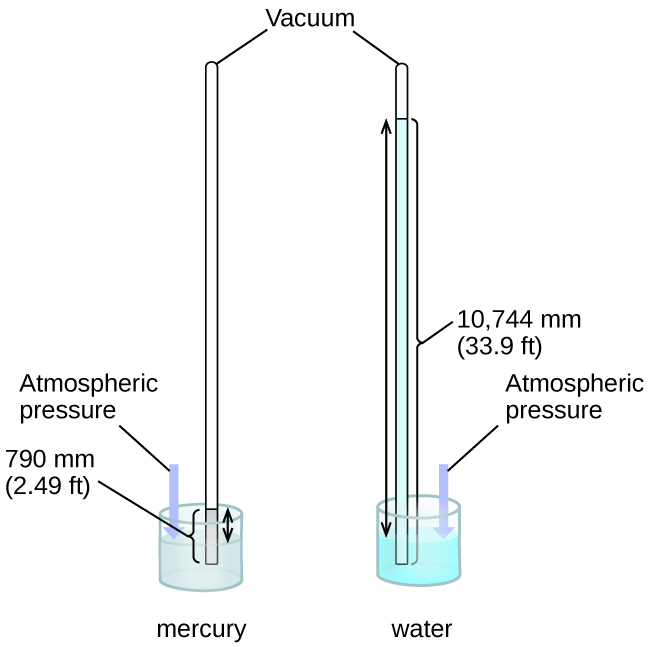
If the liquid is water, normal atmospheric pressure will back up a cavalcade of h2o over 10 meters high, which is rather inconvenient for making (and reading) a barometer. Because mercury (Hg) is nigh 13.half dozen-times denser than water, a mercury barometer but needs to be \(\frac{1}{xiii.6}\) as alpine as a water barometer—a more suitable size. Standard atmospheric pressure of one atm at sea level (101,325 Pa) corresponds to a column of mercury that is almost 760 mm (29.92 in.) loftier. The torr was originally intended to be a unit equal to one millimeter of mercury, but it no longer corresponds exactly. The force per unit area exerted by a fluid due to gravity is known as hydrostatic force per unit area, p:

\(p=h\rho grand\)

where h is the height of the fluid, ρ is the density of the fluid, and thou is acceleration due to gravity.

Calculation of Barometric Force per unit area
Show the adding supporting the claim that atmospheric pressure near ocean level corresponds to the force per unit area exerted by a column of mercury that is about 760 mm high. The density of mercury = thirteen.6 g/cm³.

Solution
The hydrostatic pressure is given past p = hρg, with h = 760 mm, ρ = 13.6 g/cm³, and yard = ix.81 m/southward^two. Plugging these values into the equation and doing the necessary unit of measurement conversions will give us the value we seek. (Annotation: Nosotros are expecting to notice a pressure level of ~101,325 Pa:)

\(101,325\phantom{\rule{0.2em}{0ex}}Due north{\text{/m}}^{2}=101,325\phantom{\dominion{0.2em}{0ex}}\frac{{\text{kg·g/s}}^{two}}{{\text{m}}^{two}}\phantom{\dominion{0.2em}{0ex}}=101,325\phantom{\rule{0.2em}{0ex}}\frac{\text{kg}}{{\text{chiliad·south}}^{2}}\)

\(p=\left(\text{760 mm}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\frac{\text{1 m}}{\text{grand mm}}\right)\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\left(\frac{\text{13.6 thou}}{1\phantom{\rule{0.2em}{0ex}}{\text{cm}}^{3}}\phantom{\dominion{0.4em}{0ex}}×\phantom{\rule{0.4em}{0ex}}\frac{\text{i kg}}{\text{yard g}}\phantom{\dominion{0.4em}{0ex}}×\phantom{\rule{0.4em}{0ex}}\frac{{\left(\text{100 cm}\correct)}^{3}}{{\left(\text{ane m}\right)}^{3}}\correct)\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\left(\frac{\text{9.81 yard}}{1\phantom{\rule{0.2em}{0ex}}{\text{s}}^{two}}\right)\)

\(=\left(\text{0.760 grand}\right)\left(13,600\phantom{\dominion{0.2em}{0ex}}{\text{kg/m}}^{iii}\right)\left(9.81\phantom{\rule{0.2em}{0ex}}{\text{m/s}}^{2}\right)=one.01\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{5}\phantom{\rule{0.2em}{0ex}}{\text{kg/ms}}^{2}=1.01\phantom{\rule{0.2em}{0ex}}×\phantom{\dominion{0.2em}{0ex}}{x}^{5}\phantom{\rule{0.2em}{0ex}}{N\text{/m}}^{ii}\)

\(=i.01\phantom{\dominion{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{x}^{5}\phantom{\rule{0.2em}{0ex}}\text{Pa}\)

Check Your Learning
Calculate the elevation of a cavalcade of water at 25 °C that corresponds to normal atmospheric pressure level. The density of h2o at this temperature is ane.0 g/cmⁱⁱⁱ.

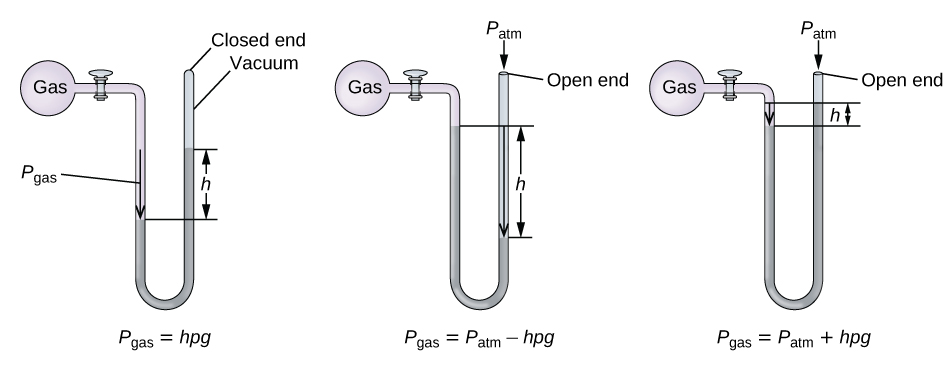
A manometer is a device similar to a barometer that tin exist used to measure out the pressure level of a gas trapped in a container. A closed-end manometer is a U-shaped tube with i closed arm, ane arm that connects to the gas to be measured, and a nonvolatile liquid (commonly mercury) in between. As with a barometer, the distance between the liquid levels in the ii arms of the tube (h in the diagram) is proportional to the pressure of the gas in the container. An open up-finish manometer ([link]) is the aforementioned as a airtight-end manometer, but one of its artillery is open to the atmosphere. In this case, the distance between the liquid levels corresponds to the departure in force per unit area between the gas in the container and the temper.

A manometer can be used to measure the pressure of a gas. The (departure in) height betwixt the liquid levels (h) is a mensurate of the pressure. Mercury is commonly used because of its large density.

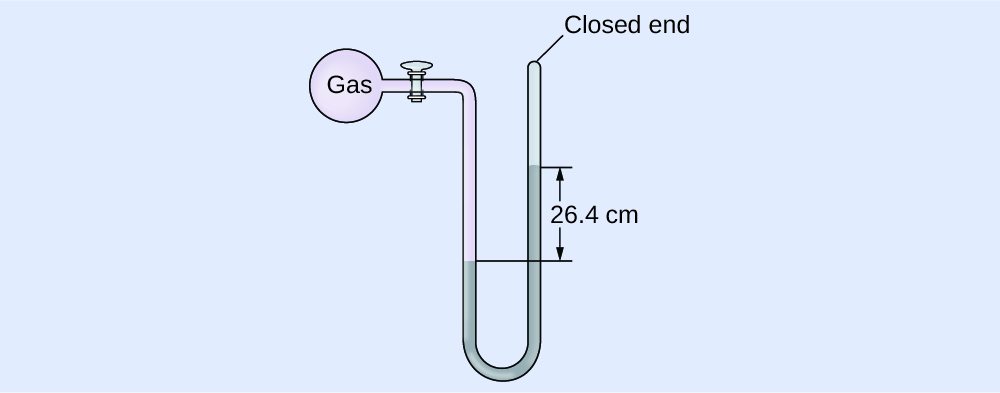
Adding of Pressure Using a Closed-Finish Manometer
The force per unit area of a sample of gas is measured with a closed-end manometer, as shown to the right. The liquid in the manometer is mercury. Decide the pressure of the gas in:

(a) torr

(b) Pa

(c) bar

Solution
The pressure of the gas is equal to a column of mercury of height 26.4 cm. (The pressure level at the bottom horizontal line is equal on both sides of the tube. The pressure level on the left is due to the gas and the pressure level on the right is due to 26.four cm Hg, or mercury.) Nosotros could use the equation p = hρg as in [link], only it is simpler to just convert between units using [link].

(a) \(26.4\phantom{\rule{0.2em}{0ex}}\overline{)\text{cm Hg}}\phantom{\dominion{0.2em}{0ex}}×\phantom{\dominion{0.2em}{0ex}}\frac{10\phantom{\dominion{0.2em}{0ex}}\overline{)\text{mm Hg}}}{1\phantom{\rule{0.2em}{0ex}}\overline{)\text{cm Hg}}}\phantom{\rule{0.4em}{0ex}}×\phantom{\rule{0.4em}{0ex}}\frac{\text{ane torr}}{1\phantom{\rule{0.2em}{0ex}}\overline{)\text{mm Hg}}}\phantom{\rule{0.2em}{0ex}}=\text{264 torr}\)

(b) \(264\phantom{\rule{0.2em}{0ex}}\overline{)\text{torr}}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\frac{i\phantom{\rule{0.2em}{0ex}}\overline{)\text{atm}}}{760\phantom{\rule{0.2em}{0ex}}\overline{)\text{torr}}}\phantom{\rule{0.4em}{0ex}}×\phantom{\dominion{0.4em}{0ex}}\frac{\text{101,325 Pa}}{1\phantom{\dominion{0.2em}{0ex}}\overline{)\text{atm}}}\phantom{\rule{0.2em}{0ex}}=\text{35,200 Pa}\)

(c) \(35\text{,200}\phantom{\rule{0.2em}{0ex}}\overline{)\text{Pa}}\phantom{\rule{0.2em}{0ex}}×\phantom{\dominion{0.2em}{0ex}}\frac{\text{1 bar}}{100,000\phantom{\rule{0.2em}{0ex}}\overline{)\text{Pa}}}\phantom{\rule{0.2em}{0ex}}=\text{0.352 bar}\)

Check Your Learning
The pressure of a sample of gas is measured with a closed-end manometer. The liquid in the manometer is mercury. Determine the pressure of the gas in:

(a) torr

(b) Pa

(c) bar

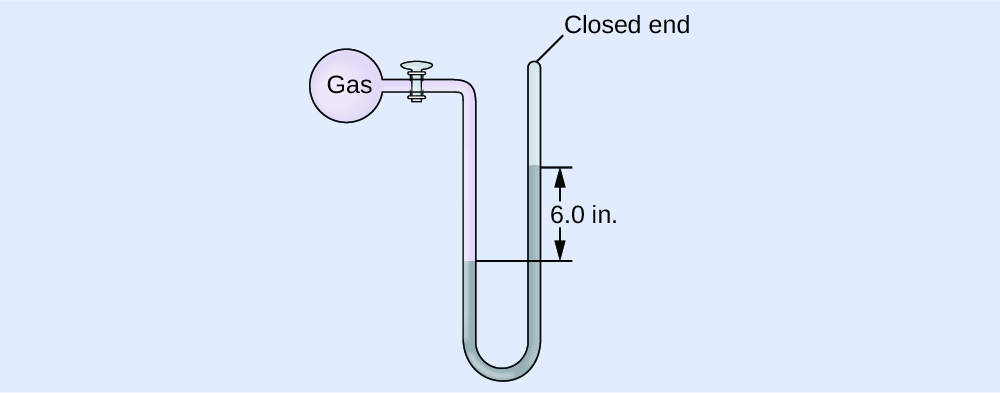
Respond:

(a) ~150 torr; (b) ~twenty,000 Pa; (c) ~0.20 bar

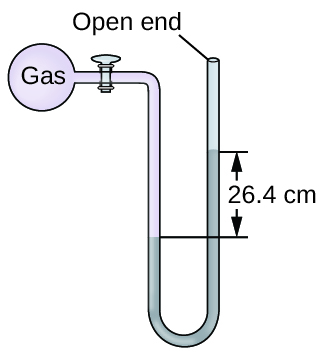
Calculation of Pressure Using an Open-Terminate Manometer
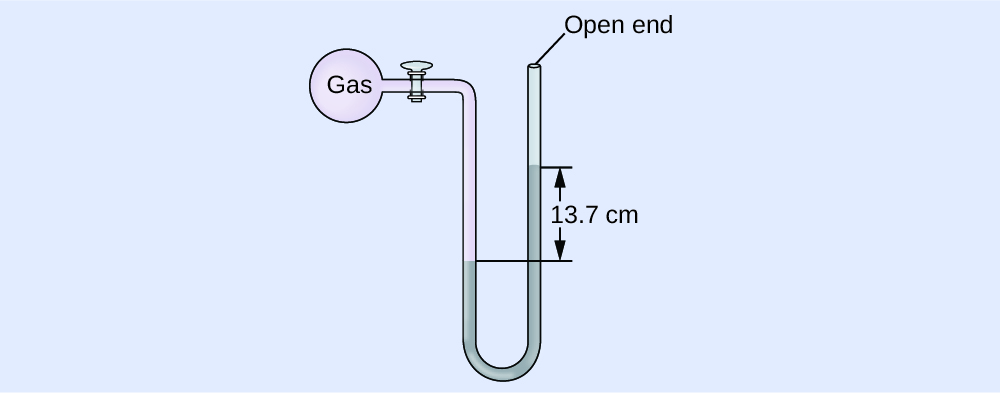
The pressure of a sample of gas is measured at bounding main level with an open-cease Hg (mercury) manometer, equally shown to the right. Determine the pressure of the gas in:

(a) mm Hg

(b) atm

(c) kPa

Solution
The pressure of the gas equals the hydrostatic pressure due to a cavalcade of mercury of peak 13.7 cm plus the pressure of the atmosphere at sea level. (The pressure at the lesser horizontal line is equal on both sides of the tube. The pressure level on the left is due to the gas and the pressure level on the correct is due to 13.seven cm of Hg plus atmospheric pressure.)

(a) In mm Hg, this is: 137 mm Hg + 760 mm Hg = 897 mm Hg

(b) \(897\phantom{\rule{0.2em}{0ex}}\overline{)\text{mm Hg}}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\frac{\text{1 atm}}{760\phantom{\rule{0.2em}{0ex}}\overline{)\text{mm Hg}}}\phantom{\dominion{0.2em}{0ex}}=\text{1.eighteen atm}\)

(c) \(1.18\phantom{\dominion{0.2em}{0ex}}\overline{)\text{atm}}\phantom{\rule{0.2em}{0ex}}×\phantom{\dominion{0.2em}{0ex}}\frac{\text{101.325 kPa}}{ane\phantom{\rule{0.2em}{0ex}}\overline{)\text{atm}}}\phantom{\rule{0.2em}{0ex}}=ane.20\phantom{\dominion{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{2}\phantom{\rule{0.2em}{0ex}}\text{kPa}\)

Check Your Learning
The pressure level of a sample of gas is measured at ocean level with an open-end Hg manometer, as shown to the right. Determine the pressure of the gas in:

(a) mm Hg

(b) atm

(c) kPa

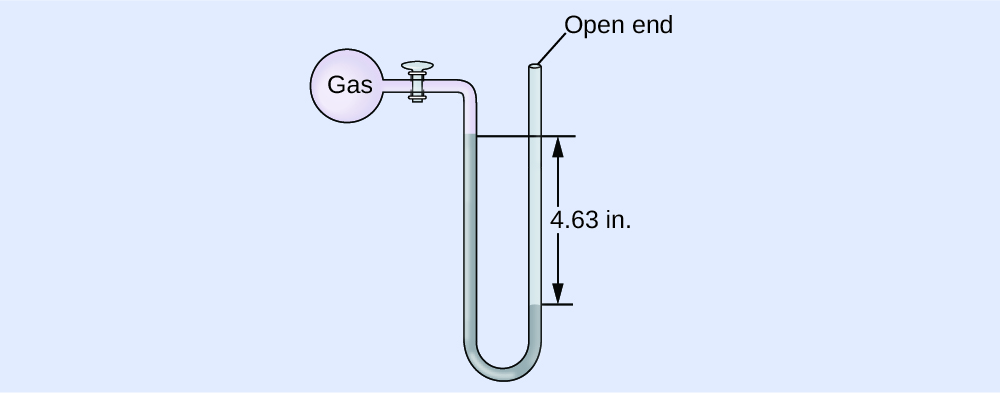
Answer:

(a) 642 mm Hg; (b) 0.845 atm; (c) 85.6 kPa

Measuring Blood Pressure

Blood pressure level is measured using a device called a sphygmomanometer (Greek sphygmos = "pulse"). It consists of an inflatable cuff to restrict claret flow, a manometer to measure the pressure, and a method of determining when blood flow begins and when it becomes impeded ([link]). Since its invention in 1881, it has been an essential medical device. At that place are many types of sphygmomanometers: manual ones that require a stethoscope and are used by medical professionals; mercury ones, used when the nigh accuracy is required; less accurate mechanical ones; and digital ones that can exist used with petty grooming just that take limitations. When using a sphygmomanometer, the cuff is placed around the upper arm and inflated until blood menstruation is completely blocked, then slowly released. As the heart beats, claret forced through the arteries causes a rise in pressure. This rise in pressure at which blood flow begins is the systolic force per unit area—the peak pressure in the cardiac cycle. When the cuff's pressure equals the arterial systolic pressure, blood flows past the cuff, creating audible sounds that can be heard using a stethoscope. This is followed by a decrease in pressure level as the heart'south ventricles prepare for another vanquish. As cuff pressure level continues to decrease, eventually sound is no longer heard; this is the diastolic pressure—the lowest pressure (resting phase) in the cardiac cycle. Blood force per unit area units from a sphygmomanometer are in terms of millimeters of mercury (mm Hg).

(a) A medical technician prepares to measure out a patient'south blood force per unit area with a sphygmomanometer. (b) A typical sphygmomanometer uses a valved rubber bulb to inflate the gage and a diaphragm gauge to measure pressure. (credit a: modification of work by Principal Sgt. Jeffrey Allen)

Meteorology, Climatology, and Atmospheric Science

Throughout the ages, people have observed clouds, winds, and precipitation, trying to discern patterns and brand predictions: when information technology is best to plant and harvest; whether information technology is safety to set out on a sea voyage; and much more. Nosotros at present face complex weather and atmosphere-related challenges that will have a major impact on our civilization and the ecosystem. Several different scientific disciplines utilize chemical principles to help us better empathize weather, the temper, and climate. These are meteorology, climatology, and atmospheric science. Meteorology is the study of the atmosphere, atmospheric phenomena, and atmospheric effects on globe's atmospheric condition. Meteorologists seek to sympathise and predict the weather in the short term, which can save lives and benefit the economy. Weather forecasts ([link]) are the effect of thousands of measurements of air pressure, temperature, and the like, which are compiled, modeled, and analyzed in weather centers worldwide.

Meteorologists use weather maps to draw and predict conditions. Regions of high (H) and depression (Fifty) pressure accept big furnishings on weather conditions. The greyness lines represent locations of constant pressure known as isobars. (credit: modification of work by National Oceanic and Atmospheric Assistants)

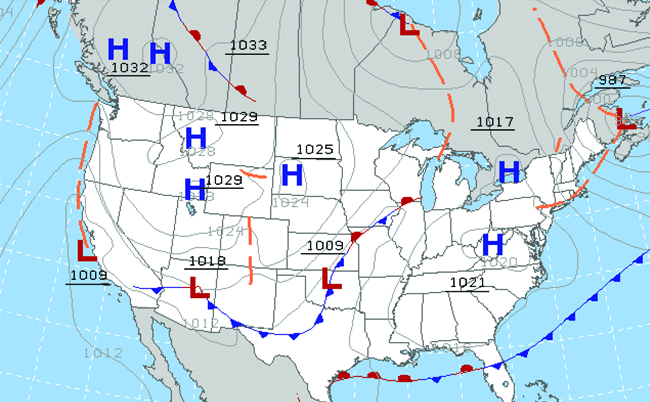
In terms of atmospheric condition, low-pressure systems occur when the globe's surface atmospheric pressure is lower than the surrounding environment: Moist air rises and condenses, producing clouds. Movement of moisture and air inside various weather fronts instigates most weather events.

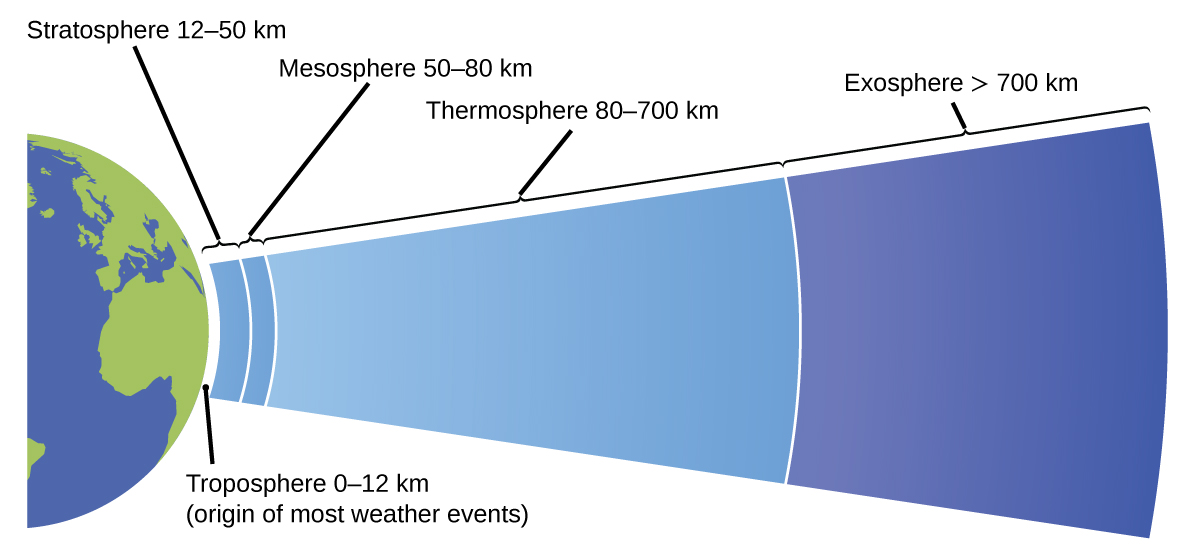
The atmosphere is the gaseous layer that surrounds a planet. Globe'due south atmosphere, which is roughly 100–125 km thick, consists of roughly 78.one% nitrogen and 21.0% oxygen, and can be subdivided farther into the regions shown in [link]: the exosphere (furthest from globe, > 700 km above sea level), the thermosphere (lxxx–700 km), the mesosphere (l–fourscore km), the stratosphere (2nd lowest level of our atmosphere, 12–50 km to a higher place sea level), and the troposphere (upwardly to 12 km above sea level, roughly fourscore% of the earth'south temper by mass and the layer where most weather condition events originate). As y'all get higher in the troposphere, air density and temperature both decrease.

Earth'southward atmosphere has five layers: the troposphere, the stratosphere, the mesosphere, the thermosphere, and the exosphere.

Climatology is the study of the climate, averaged weather conditions over long fourth dimension periods, using atmospheric data. However, climatologists study patterns and effects that occur over decades, centuries, and millennia, rather than shorter time frames of hours, days, and weeks similar meteorologists. Atmospheric scientific discipline is an even broader field, combining meteorology, climatology, and other scientific disciplines that report the temper.

Key Concepts and Summary

Gases exert pressure level, which is force per unit of measurement expanse. The pressure of a gas may be expressed in the SI unit of measurement of pascal or kilopascal, as well every bit in many other units including torr, atmosphere, and bar. Atmospheric pressure is measured using a barometer; other gas pressures can exist measured using one of several types of manometers.

Fundamental Equations

• \(P=\phantom{\rule{0.2em}{0ex}}\frac{F}{A}\)
• p = hρg

Chemistry Cease of Chapter Exercises

Why are sharp knives more constructive than tiresome knives (Hint: think about the definition of pressure)?

The cutting edge of a pocketknife that has been sharpened has a smaller surface expanse than a dull knife. Since force per unit area is force per unit area, a abrupt knife will exert a college pressure with the same amount of strength and cut through material more effectively.

Why do some modest bridges have weight limits that depend on how many wheels or axles the crossing vehicle has?

Why should yous scroll or abdomen-crawl rather than walk across a thinly-frozen pond?

Lying down distributes your weight over a larger surface surface area, exerting less pressure on the ice compared to standing up. If you exert less pressure level, you are less likely to break through thin ice.

A typical barometric pressure in Redding, California, is nigh 750 mm Hg. Calculate this pressure in atm and kPa.

A typical barometric force per unit area in Denver, Colorado, is 615 mm Hg. What is this pressure in atmospheres and kilopascals?

0.809 atm; 82.0 kPa

A typical barometric pressure in Kansas Urban center is 740 torr. What is this pressure level in atmospheres, in millimeters of mercury, and in kilopascals?

Canadian tire pressure gauges are marked in units of kilopascals. What reading on such a estimate corresponds to 32 psi?

two.2 \(×\) x² kPa

During the Viking landings on Mars, the atmospheric pressure was determined to be on the average about 6.l millibars (ane bar = 0.987 atm). What is that pressure in torr and kPa?

The pressure level of the atmosphere on the surface of the planet Venus is nigh 88.eight atm. Compare that pressure in psi to the normal pressure on earth at sea level in psi.

World: 14.7 lb in^–2; Venus: thirteen.i\(×\) 10ⁱⁱⁱ lb in⁻²

A medical laboratory catalog describes the pressure level in a cylinder of a gas equally 14.82 MPa. What is the pressure of this gas in atmospheres and torr?

Consider this scenario and answer the following questions: On a mid-August day in the northeastern United States, the following information appeared in the local newspaper: atmospheric pressure at sea level 29.97 in. Hg, 1013.9 mbar.

(a) What was the pressure in kPa?

(b) The pressure well-nigh the seacoast in the northeastern United States is normally reported most 30.0 in. Hg. During a hurricane, the pressure may fall to virtually 28.0 in. Hg. Calculate the driblet in pressure in torr.

(a) 101.five kPa; (b) 51 torr drop

Why is it necessary to utilise a nonvolatile liquid in a barometer or manometer?

The pressure of a sample of gas is measured at ocean level with a closed-end manometer. The liquid in the manometer is mercury. Make up one's mind the pressure of the gas in:

(a) torr

(b) Pa

(c) bar

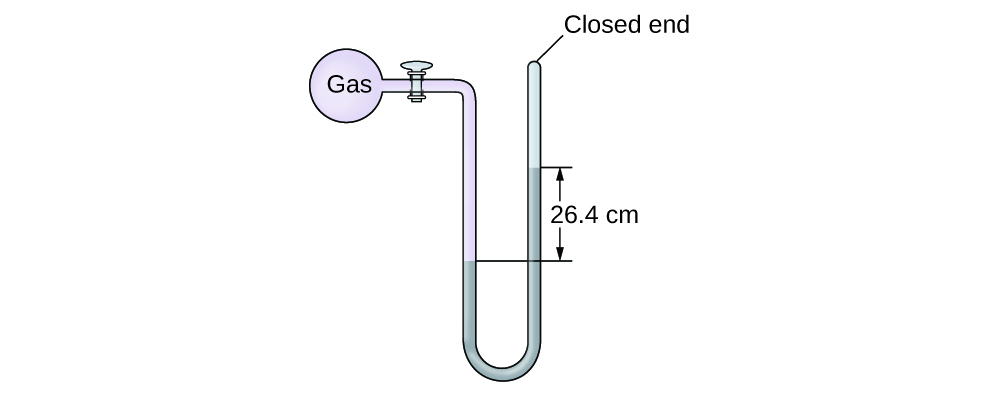
(a) 264 torr; (b) 35,200 Pa; (c) 0.352 bar

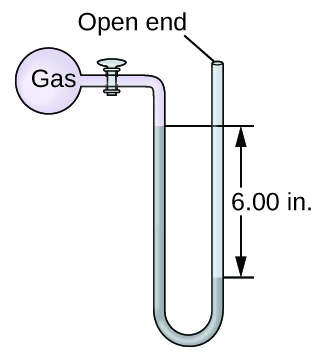
The pressure of a sample of gas is measured with an open-end manometer, partially shown to the right. The liquid in the manometer is mercury. Assuming atmospheric pressure is 29.92 in. Hg, determine the pressure of the gas in:

(a) torr

(b) Pa

(c) bar

The pressure of a sample of gas is measured at sea level with an open-end mercury manometer. Assuming atmospheric force per unit area is 760.0 mm Hg, determine the pressure of the gas in:

(a) mm Hg

(b) atm

(c) kPa

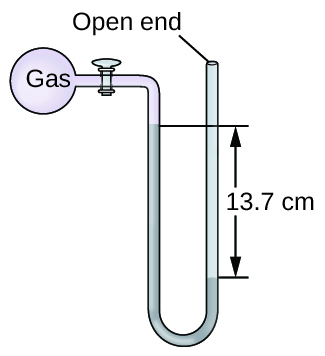
(a) 623 mm Hg; (b) 0.820 atm; (c) 83.one kPa

The pressure of a sample of gas is measured at body of water level with an open up-end mercury manometer. Bold atmospheric pressure is 760 mm Hg, make up one's mind the pressure of the gas in:

(a) mm Hg

(b) atm

(c) kPa

How would the employ of a volatile liquid impact the measurement of a gas using open up-ended manometers vs. closed-end manometers?

With a airtight-cease manometer, no alter would exist observed, since the vaporized liquid would contribute equal, opposing pressures in both arms of the manometer tube. However, with an open up-ended manometer, a college pressure reading of the gas would exist obtained than expected, since P _gas = P _atm + P _{vol liquid}.

Glossary

temper (atm)

unit of measurement of pressure level; 1 atm = 101,325 Pa

bar

(bar or b) unit of pressure; i bar = 100,000 Pa

barometer

device used to measure atmospheric pressure

hydrostatic pressure level

pressure exerted by a fluid due to gravity

manometer

device used to measure the pressure of a gas trapped in a container

pascal (Pa)

SI unit of pressure; one Pa = 1 Due north/g²

pounds per square inch (psi)

unit of pressure common in the Us

pressure

strength exerted per unit area

torr

unit of pressure level; \(\text{1 torr}=\phantom{\rule{0.2em}{0ex}}\frac{i}{760}\phantom{\rule{0.2em}{0ex}}\text{atm}\)

bailyfroultan1957.blogspot.com

Source: https://pressbooks-dev.oer.hawaii.edu/chemistry/chapter/gas-pressure/

Share this post